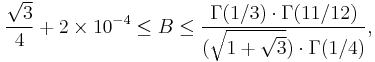Bloch's theorem (complex variables)
In complex analysis, a field within mathematics, Bloch's theorem is a result that gives a lower bound on the size of the image of a certain class of holomorphic functions. It is named after André Bloch.
Statement
Let ƒ be a holomorphic function on a region (i.e. an open, connected subset of C) that includes as a subset the closed unit disk |z| ≤ 1. Suppose ƒ(0) = 0 and ƒ ′(0) = 1. Let b(ƒ) be the supremum of those numbers r such that there is a subregion S of the open unit disk |z| < 1 on which ƒ is injective and such that ƒ(S) contains a disk of radius r. Then b(ƒ) ≥ 1/72.
Bloch's constant
The lower bound 1/72 is not the best possible. The number B defined as the infimum of all b(ƒ) where ƒ satisfies the hypotheses of Bloch's theorem is called Bloch's constant. Bloch's theorem tells us B ≥ 1/72, but its exact value is still unknown.
The best known bounds for B at present are
where Γ is the Gamma function. The lower bound was proved by Chen and Gauthier, and the upper bound dates back to Ahlfors and Grunsky.
In their paper, Ahlfors and Grunsky conjectured that their upper bound is actually the true value of B.
References
- Ahlfors, Lars Valerian; Grunsky, H. (1937). "Über die Blochsche Konstante". Mathematische Zeitschrift 42 (1): 671–673. doi:10.1007/BF01160101.
- Baernstein, Albert II; Vinson, Jade P. (1998). "Local minimality results related to the Bloch and Landau constants". Quasiconformal mappings and analysis. Ann Arbor: Springer, New York. pp. 55–89.
- Bloch, André (1925). "Les théorèmes de M.Valiron sur les fonctions entières et la théorie de l'uniformisation". Annales de la faculté des sciences de l'Université de Toulouse 17 (3): 1–22. ISSN 0240-2963.
- Chen, Huaihui; Gauthier, Paul M. (1996). "On Bloch's constant". Journal d'Analyse Mathématique 69 (1): 275–291. doi:10.1007/BF02787110.